Spin and Spin Again in R Probability Questionb
Learn About Calculating Probability With The Following Examples And Interactive Exercises.
Trouble: A spinner has 4 equal sectors colored yellow, blueish, light-green and red. What are the chances of landing on blue subsequently spinning the spinner? What are the chances of landing on scarlet?
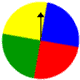
Solution: The chances of landing on blue are 1 in 4, or 1 4th.
The chances of landing on red are 1 in 4, or 1 fourth.
This problem asked usa to find some probabilities involving a spinner. Let'southward look at some definitions and examples from the problem above.
| Definition | Instance |
| Anexperiment is a situation involving chance or probability that leads to results called outcomes. | In the trouble in a higher place, the experiment is spinning the spinner. |
| Anupshot is the result of a single trial of an experiment. | The possible outcomes are landing on yellow, bluish, dark-green or cerise. |
| Aneffect is ane or more outcomes of an experiment. | One outcome of this experiment is landing on blue. |
| Probability is the measure of how likely an event is. | The probability of landing on blue is one fourth. |
In lodge to measure probabilities, mathematicians take devised the post-obit formula for finding the probability of an effect.
| Probability Of An Event | |||
|
The probability of issue A is the number of ways event A can occur divided by the total number of possible outcomes. Let's accept a expect at a slight modification of the problem from the acme of the page.
Experiment one: A spinner has 4 equal sectors colored yellow, blue, green and red. After spinning the spinner, what is the probability of landing on each color?
The possible outcomes of this experiment are xanthous, bluish, light-green, and crimson.
Probabilities:
| P(yellow) | = | # of ways to land on yellow | = | one |
| total # of colors | 4 | |||
| P(blueish) | = | # of means to state on blue | = | 1 |
| total # of colors | 4 | |||
| P(greenish) | = | # of ways to country on light-green | = | 1 |
| total # of colors | 4 | |||
| P(red) | = | # of ways to land on red | = | 1 |
| total # of colors | 4 | |||
Experiment 2: A single half dozen-sided die is rolled. What is the probability of each outcome? What is the probability of rolling an even number? of rolling an odd number?
Outcomes: The possible outcomes of this experiment are i, 2, 3, four, v and 6.
Probabilities:
| P(ane) | = | # of ways to roll a 1 | = | ane | ||
| full # of sides | six | |||||
| P(2) | = | # of means to roll a 2 | = | one | ||
| total # of sides | half dozen | |||||
| P(3) | = | # of means to roll a iii | = | 1 | ||
| total # of sides | 6 | |||||
| P(4) | = | # of means to roll a four | = | 1 | ||
| full # of sides | 6 | |||||
| P(5) | = | # of means to roll a five | = | 1 | ||
| total # of sides | half-dozen | |||||
| P(6) | = | # of ways to roll a vi | = | 1 | ||
| total # of sides | 6 | |||||
| P(even) | = | # ways to roll an even number | = | 3 | = | one |
| total # of sides | vi | two | ||||
| P(odd) | = | # ways to roll an odd number | = | 3 | = | 1 |
| total # of sides | 6 | 2 | ||||
Experiment 2 illustrates the difference between an outcome and an event. A single result of this experiment is rolling a 1, or rolling a 2, or rolling a 3, etc. Rolling an even number (ii, 4 or half-dozen) is an result, and rolling an odd number (i, 3 or 5) is also an consequence.
In Experiment ane the probability of each effect is always the same. The probability of landing on each color of the spinner is always 1 quaternary. In Experiment ii, the probability of rolling each number on the die is always ane 6th. In both of these experiments, the outcomes are equally likely to occur. Allow's look at an experiment in which the outcomes are non equally probable.
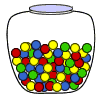Experiment 3: A glass jar contains 6 reddish, 5 dark-green, 8 blue and 3 yellow marbles. If a unmarried marble is chosen at random from the jar, what is the probability of choosing a red marble? a green marble? a blueish marble? a yellow marble?
Outcomes: The possible outcomes of this experiment are cherry, green, blue and yellowish.
Probabilities:
| P(red) | = | # of ways to choose carmine | = | vi | = | iii |
| total # of marbles | 22 | 11 | ||||
| P(green) | = | # of ways to choose green | = | 5 | ||
| total # of marbles | 22 | |||||
| P(blue) | = | # of means to choose blue | = | eight | = | four |
| total # of marbles | 22 | eleven | ||||
| P(yellow) | = | # of ways to choose yellow | = | 3 | ||
| total # of marbles | 22 | |||||
The outcomes in this experiment are not equally likely to occur. Y'all are more likely to choose a blue marble than any other colour. You are least likely to choose a yellowish marble.
Experiment 4: Choose a number at random from 1 to five. What is the probability of each outcome? What is the probability that the number chosen is fifty-fifty? What is the probability that the number chosen is odd?
Outcomes: The possible outcomes of this experiment are 1, two, 3, 4 and 5.
Probabilities:
| P(ane) | = | # of ways to choose a 1 | = | ane |
| total # of numbers | 5 | |||
| P(ii) | = | # of ways to choose a 2 | = | 1 |
| total # of numbers | 5 | |||
| P(3) | = | # of means to choose a three | = | 1 |
| full # of numbers | 5 | |||
| P(4) | = | # of ways to choose a 4 | = | 1 |
| total # of numbers | v | |||
| P(5) | = | # of means to choose a v | = | 1 |
| full # of numbers | 5 | |||
| P(fifty-fifty) | = | # of ways to choose an fifty-fifty number | = | ii |
| full # of numbers | 5 | |||
| P(odd) | = | # of ways to cull an odd number | = | 3 |
| total # of numbers | 5 | |||
The outcomes 1, 2, 3, four and 5 are every bit likely to occur as a event of this experiment. However, the events even and odd are not as probable to occur, since there are 3 odd numbers and but two fifty-fifty numbers from 1 to 5.
Summary: The probability of an outcome is the measure of the run a risk that the event will occur every bit a result of an experiment. The probability of an event A is the number of ways event A can occur divided by the full number of possible outcomes. The probability of an issue A, symbolized by P(A), is a number betwixt 0 and 1, inclusive, that measures the likelihood of an consequence in the following way:
- If P(A) > P(B) and then event A is more likely to occur than event B.
- If P(A) = P(B) and then events A and B are every bit likely to occur.
Exercises
Directions: Read each question below. Select your answer by clicking on its button. Feedback to your reply is provided in the RESULTS BOX. If you make a mistake, cull a different button.
| i. | Which of the following is an experiment? |
| two. | Which of the following is an outcome? |
| 3. | Which of the following experiments does NOT have equally likely outcomes? |
| iv. | What is the probability of choosing a vowel from the alphabet? |
| 5. | A number from 1 to eleven is chosen at random. What is the probability of choosing an odd number? |
Sign Upwards For Our Complimentary Newsletter!
Sign Up For Our Gratis Newsletter!
Source: https://www.mathgoodies.com/lessons/vol6/intro_probability
0 Response to "Spin and Spin Again in R Probability Questionb"
Post a Comment